이러한 표본조사란 무엇이며, 어떻게 이루어질까요? 표본조사는 조사하고 싶은 대상 중 일부를 선택하여 조사하고, 그 결과를 통해 전체를 유추하는 방법을 말합니다. 전체를 조사하는 것이 아닌, 일부만을 조사하기 때문에 어떤 표본을 뽑느냐가 매우 중요하죠. 가장 대표적인 표본조사의 사례는 ‘여론조사’입니다. 투표를 마치고 나올 때, 여론조사 질문을 받아 본 경험이 있으실 겁니다. 선거를 시행할 때, 그 결과를 예측하기 위해 각 방송사 등에서는 여론조사를 실시합니다. 전수조사라고 볼 수 있는 선거 개표에 앞서, 일부 사람들을 대상으로 결과를 물어보고 그 결과로 당선인을 예측하는 것이죠. 이때 특정 나이대, 특정 성별만을 대상으로 여론조사를 한다면 실제와는 다른 결과를 얻을 수도 있습니다. 그래서 ‘표본’이 중요한 것입니다.
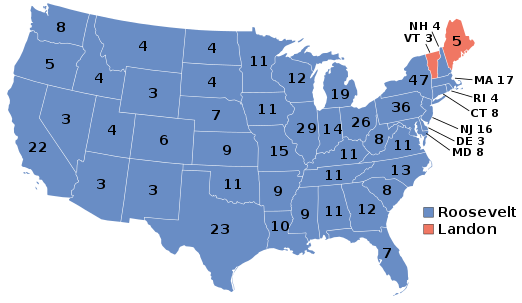
잘못된 표본 선정으로 인해 여론조사가 실패했던 대표적인 사례는 1936년 미국 대선 여론조사입니다. 당시 잡지사 ‘리터러리 다이제스트’는 자동차등록부, 전화번호부 등에서 얻은 주소로 가상투표 용지를 보내 236만 명의 표본을 얻었고, 공화당 후보였던 앨프리드 랜던이 민주당의 프랭클린 루스벨트를 꺾을 것이라고 예측했습니다. 하지만 실제로는 루스벨트가 60%가 넘는 표를 받고 당선되었죠. 표본이 전체를 대변하지 못하고, 공화당을 지지할 확률이 높은 자동차와 전화가 있는 부유층 사람들이 주를 이루었다는 것이 문제였습니다.
그렇다면 원하는 결과를 얻기 위해, 어떻게 표본을 뽑아야 할까요? 그냥 랜덤으로 뽑으면 될까요? 오늘은 표본을 선정하는 대표적인 방법들에 대해서 알아보고, 그 각각의 장단점 및 효율성에 대해 생각해봅시다.
가장 기본적인 방법,
단순임의추출(SRS)
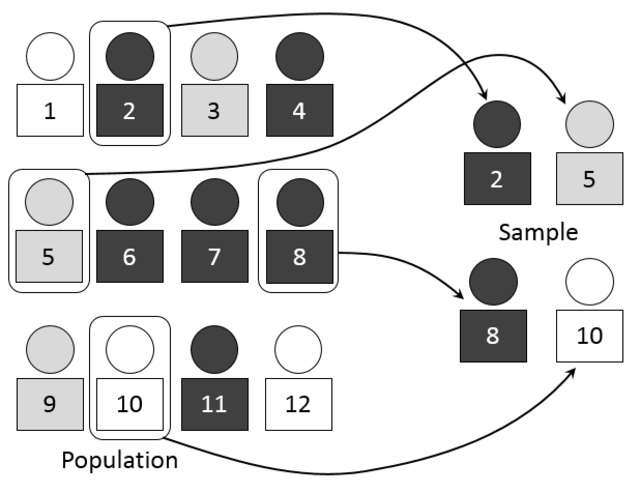
단순임의추출(Simple Random Sampling, SRS)은 가장 기본적이고 쉬운 표본추출법이라고 할 수 있습니다. 대상 집단의 각각의 원소를 동일한 확률로 추출하는 방법을 말합니다. 이름에서 알 수 있듯이, 아무런 조작 없이 ‘랜덤’으로 뽑는 방법인 셈입니다. 간단한 방법인 만큼 조사에 드는 비용을 줄일 수 있다는 장점이 있는 방법, 표본이 고르지 못한 경우 조사의 효율성이 떨어진다는 단점도 있습니다.
어떤 경우에 단순임의추출법을 사용하면 될까요? 예를 들어, A 학교 학생들의 평균 컴퓨터 사용 시간을 조사해본다고 할 때, 1~3학년까지 500명씩 있다고 가정하면 전체 1,500명의 학생의 평균을 조사하면 됩니다. 하지만 1500명을 모두 조사하는 것은 꽤 비효율적인 일입니다. 그래서 1,500명 중 랜덤으로 150명만 뽑아서 조사하고, 이를 바탕으로 전체 학생의 평균, 즉 모평균을 추정하게 됩니다. 이때 주의할 점은, 표본 조사에서 추정을 할 때에는 하나의 값을 추정하는 것이 아니라, 분산 값을 이용하여 구간으로 추정을 한다는 것입니다. 위의 예시 상황에서 150명의 평균이 전체의 평균과 어느 정도 일치한다는 것을 예상할 수 있겠죠?
비슷한 그룹을 나누어서,
층화추출
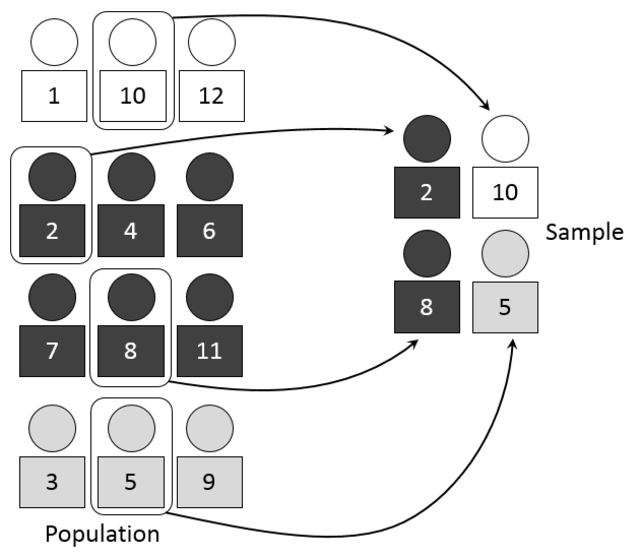
조사하고 싶은 대상들의 특성이 그룹별로 다르다면 어떻게 조사하는 것이 좋을까요? 예를 들어 위의 상황에서, 1학년에 비해 3학년 학생들의 평균 컴퓨터 사용시간이 현저히 적다고 생각해봅시다. 전체에서 뽑은 150명의 표본에 1학년 학생들이 많다면, 잘못된 추정을 하게 되지 않을까요?
이럴 때 사용할 수 있는 것이 바로 ‘층화추출’입니다. 층화추출이란 표본 안에서 그룹별로 특성이 매우 다를 경우, 그 그룹을 층으로 나누는 ‘층화’ 과정을 거친 후 각 층에서 단순임의추출을 하는 방법을 말합니다. 같은 층 안의 원소들끼리는 유사하고, 층과 층 사이에는 이질적이어야 이러한 층화추출이 의미를 가지게 됩니다. 층화추출은 단순임의추출에 비해 관리가 쉽고 비용이 낮아지는 효과가 있습니다. 하지만 ‘층’에 대한 정보가 추가적으로 필요하고, 이 층을 나누는 기준이 모호할 경우들도 있어 항상 효율적이라고는 할 수 없다는 단점도 가지고 있습니다.
이러한 층화추출의 대표적인 예시는 여론조사할 때 지역, 연령, 성별에 따라 나누어 조사를 하는 것이라고 할 수 있습니다. 지역, 연령, 성별은 정치적 성향이 달라질 수 있는 대표적인 ‘층’의 기준이라고 할 수 있죠. 이러한 층에 따라 결과가 달라질 수 있기 때문에, 여론조사를 할 때에는 각 층에 맞는 인원을 조사하거나, 조사한 인원에 대해 층에 해당하는 가중치 조정을 통해 전체 결과를 예측하게 됩니다. 이렇게 조사하면 랜덤으로 조사할 때에 비해 훨씬 정확한 결과를 얻을 수 있겠죠?
일부 그룹만 조사한다,
집락추출
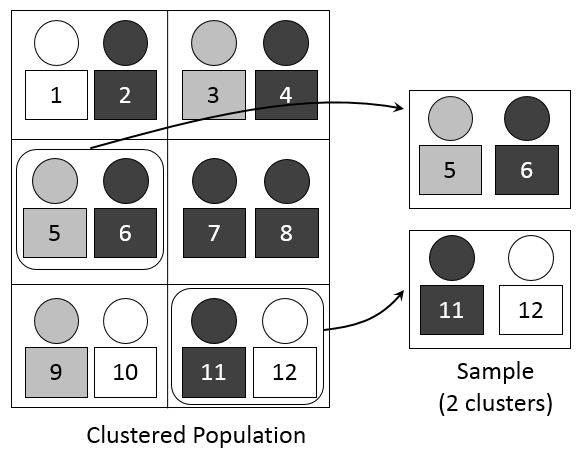
마지막으로 알아볼 방법은 ‘집락추출’입니다. 집락추출이란, 전체 모집단을 그룹들로 나누고, 일부 그룹들만을 선택하여 조사하는 방법입니다. 다시 단순임의추출에서 살펴본 학교 상황으로 돌아가볼까요? 1~3학년 전체 학생들의 평균 컴퓨터 사용 시간을 조사할 때, 우리는 각 학급별 평균 컴퓨터 사용 시간은 비슷할 것이라고 생각할 수 있습니다. 그렇다면, 각 학년별로 1반만 선택해서 조사하는 것이 가능하겠죠. 이처럼 집락 내의 원소들은 이질적이고, 집락 간은 동질적일 경우 집락표집은 효과를 보이게 됩니다.
전체에 대해 조사하는 것이 아닌 일부 집락에 대해서만 조사하면 되기 때문에, 집락추출은 비용이나 시간 면에서 굉장히 효율적이라는 장점이 있습니다. 하지만 전체를 대상으로 조사할 때의 비해 추정의 정확도가 떨어진다는 단점이 있습니다. 집락 추출의 경우, 집락 내의 모든 원소를 조사할 수도 있지만 대규모의 표본 조사 경우에는 그 집락 안에서도 추출을 하는 이차집락추출 등의 방법들을 추가적으로 사용할 수도 있습니다.
지금까지 단순임의추출, 층화추출, 집락추출이라는 세 가지 표본추출 방법에 대하여 알아보았는데요. 이외에도 계통표집 등의 확률표집 방법들이 있습니다. 뿐만 아니라 할당표집, 의도적표집 등 비확률표집 방법들과 같이 다양한 기술들이 존재합니다.
이러한 다양한 방법들은 모두 ‘어떻게 하면 더 효율적으로, 정확하게 표본 조사를 할 수 있을까?’라는 질문에 대한 답을 찾아가는 과정에서 제시된 방법들인데요. 이 질문에 답하기 위해 각 표집 방법을 필요에 따라 적절히 결합해 사용하거나, 통계적인 방법을 이용해 보정하는 등 더 정확한 예측을 위한 기술들은 계속해서 제시되고 발전하고 있습니다. 앞으로도 어떻게 하면 데이터가 세상을 더 정확하게 설명할 수 있을지 기대되네요!